2-4 神经网络的“引擎”：基于梯度的优化

随机初始化：选择权重较小的矩阵进行运算。

训练：逐步调节

训练循环：

• 抽取训练样本x和对应目标y_true组成的一个数据批量
• 在x上运行模型，得到y_pred（向前传播）
• 计算损失值，用于衡量y_pred和y_true之间的差距
• 更新模型的所有权重，以略微减小模型在这批数据上的损失值。

2.4.1 导数

$$f(x) = y$$

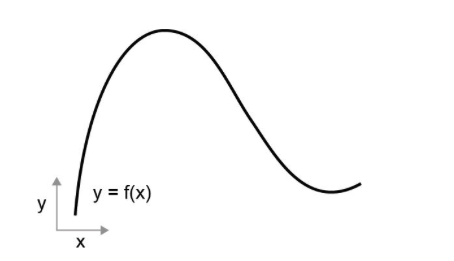
函数是连续的，x增加很小的epsilon,y也发生微小变化。

f(x + epsilon_x) = y + a * epsilon_x

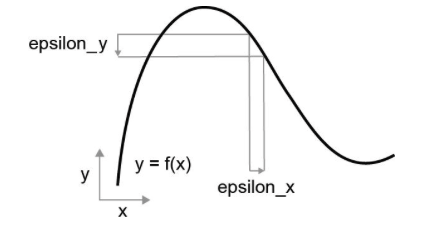
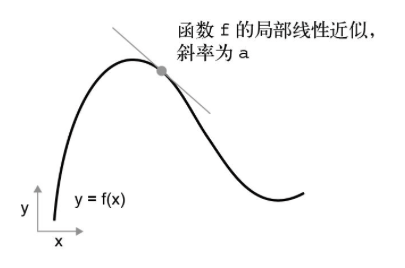
x足够接近p时，近似认为是斜率

斜率a时f在p点的导数

2.4.2 张量运算的导数：梯度

标量元组(x,y)映射一个标量值z，可以绘制三维空间（以x、y、z为坐标轴）中的二维表面。

张量运算的导数叫做梯度（gradient）.

对于标量函数，导数表示曲线的局部斜率(local slope)是加入了epsilon,epsilon足够小时，接近斜率。

张量函数的梯度表示该函数所对应多维表面的曲率(curvature)。

以机器学习中的一个例子为展示：

• 输入向量x（数据集的一个样本）
• 矩阵W(模型权重)
• 目标值y_true(模型应该学到的与x相关的结果)
• 一个损失函数loss(用于衡量模型当前预测值与y_true之间的差距)

可以用W来计算预测值y_pre，然后计算损失值，即预测值y_pre与目标值y_true之间的差距

y_pred = dot(W,x) #利用模型权重w对x进行预测
loss_value = loss(y_pred,y_true) #估算预测值的偏差有多大

用梯度更新W，以使loss_value变小

保持输入数据x和y_true不变，可以讲前面的运算看作一个将模型权重W的值映射到损失值的函数

loss_value = f(w) #f描述的是：当W变化时，损失值所形成的曲线（或高维表面）

假设W的当前值为W0，f在W0点的导数是一个张量grad(loss_value,W0)

其形状与W相同，每个元素grad(loss_value,W0)[i][j]表示当W0[i][j]发生变化时loss_value变化的方向和大小。张量grad(loss_value,W0)函数f(w)=loss_value在W0处的梯度，也叫做loss_value相对于W在W0附近的梯度。

偏导数

张量运算grad(f(W),W)以矩阵W为输入，它可以表示为标量函数grad_ij(f(w),w_ij)的组合，每个标量函数返回的是loss_value = f(W)相对于W[i,j]的导数。（假设W的其他所有元素都不变）

grad_ij叫作f对于W[i,j]的偏导数。(partial derivative)。

grad(loss_value,W0)具体含义：

单变量函数f(x)的导数可以看做函数f曲线的斜率，同样的，grad(loss_value,W0)可以看作表示loss_value = f(W)在W0附近最陡上升方向的张量，也表示这一上升方向的斜率。每个偏导数表示f在某个方向的斜率。

对于一个函数f(x)沿着导数的反方向移动可以进一步减小f(x)的值，同样对于一个张量f(W)，可以将W沿着梯度的反方向移动来减小loss_value = f(W)

比如：

W1 = W0 - step * grad(f(W0),W0)

step是一个很小的比例因子。

沿着f最陡上升的反方向移动，直观上可以移动到曲线上更低的位置。

注意：比例因子step是必须的，因为grad(loss_value,W0)只是W0附近曲率的近似值，所以不能离W0太远。

2.4.3 随机梯度下降

可微函数的最小值在导数为0处

应用于神经网络之中，通过对grad(f(W),W) = 0求解W来实现。

但是在实际神经网络中无法求解，参数的个数成千上万个。

小批量随机梯度下降（小批量SGD）

stochastic = random

1. 抽取训练样本x和对应目标的y_true组成一个数据批量
2. 在x上运行模型，得到预测值y_pred（向前传播）
3. 计算损失值，衡量y_pred和y_true之间的差距
4. 计算损失相对于模型参数的梯度(反向传播)
5. 将参数沿着梯度的反方向移动一小步，比如W-=learning_rate * gradient，从而使这批数据上的损失值减小一点。学习率（learning_rate)是一个调节梯度下降速度的标量因子。

小批量SGD算法的一个变体每次迭代只选取一个样本和目标，而不是抽取一批数据。

这是真SGD，有别于小批量SGD。

另一种极端，批量梯度下降，每次迭代在所有数据上。

SGD的多种变体

• 带动量的SGD
• Adagrad
• RMSprop

这些变体在计算下一次权重更新时，不仅要考虑当前的梯度值，还要考虑上一次权重的更新，这些方法被称为优化方法（optimization method）或者优化器（optimizer）。

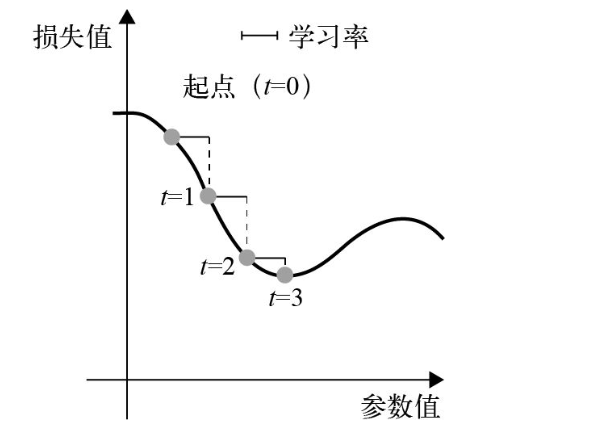
动量SGD

解决了两个问题：

• 收敛速度
• 局部极小值

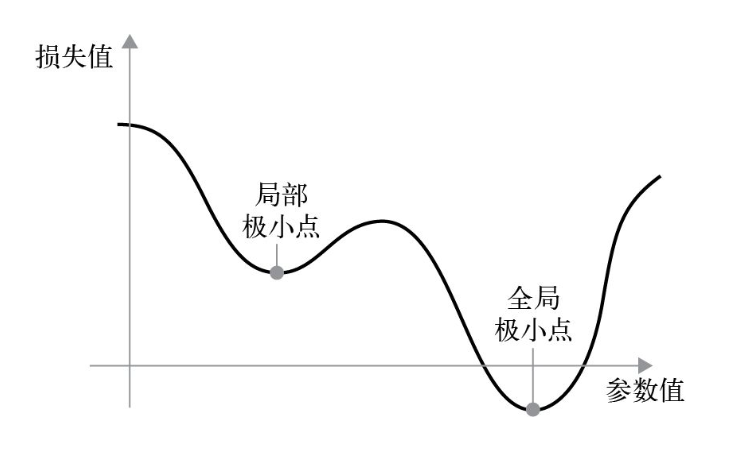
在图中局部极小点处，左移和右移都会导致损失值的增大，所以使用learning_rate较小的SGD对参数进行优化，优化过程会陷入到局部极小点，而无法找到全局极小点。

使用动量方法，参考物理，每次移动小球，不仅考虑它的当前加速度，还考虑它的速度。

实践意义：更新W时不仅考虑当前的梯度值，还要考虑上一次参数更新。

past_velocity = 0.
momentum = 0.1   ←---- 不变的动量因子
while loss > 0.01:   ←---- 优化循环
    w, loss, gradient = get_current_parameters()
    velocity = past_velocity * momentum - learning_rate * gradient
    w = w + momentum * velocity - learning_rate * gradient
    past_velocity = velocity
    update_parameter(w)

2.4.4 链式求导：反向传播算法

双层模型，计算损失相对于权重的梯度，使用反向传播算法。

01.链式法则

利用简单运算的导数，可以轻松算出这些基本运算的任意复杂组合的梯度。

神经网络由许多链接在一起的张量运算组成，每个张量运算的的导数已知，且都很简单。

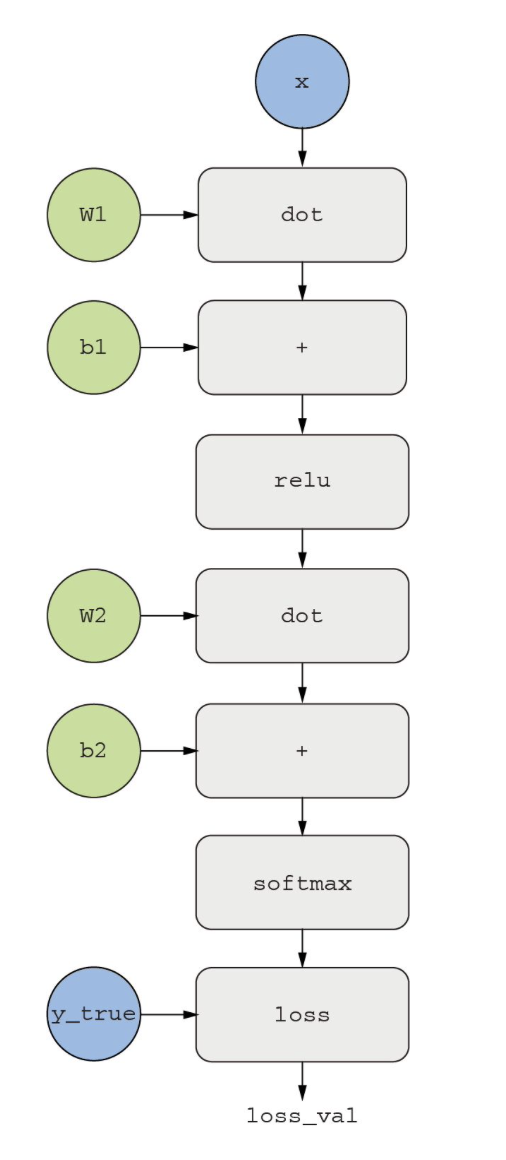
代码清单2-2中定义的模型，一个由变量W1、b1、W2、b2（分别属于第一个Dense层和第二个Dense层）参数化的函数，运用到的基本运算是dot、relu、sotfmax和+，以及损失函数loss。

loss_value = loss(y_true, softmax(dot(relu(dot(inputs, W1) + b1), W2) + b2))

链式法则求导（Chain Rule）

两个函数f和g复合。

复合函数：

$$fg:fg(x)==f(g(x))$$

def fg(x):
  x1 = g(x)
  y = f(x1)
  return y

链式法则规定：$grad(y,x) = grad(y,x1) * grad(x1,x)$

知道f和g的导数，就能求出fg的导数，添加多个函数就像一条链，因此称为链式法则。

def fghj:
  x1 = j(x)
  x2 = g(x1)
  x3 = h(x2)
  y = f(x3)
  return y
grad(y,x) = (grad(y,x3),grad(x3,x2),grad(x2,x1),grad(x1,x))

将链式法则应用于神经网络梯度值的计算，就得到了一种叫作反向传播的算法。

02 用计算图自动划分

计算图是思考反向传播算法的一种有用方法，深度学习的核心数据结构，由运算构成的有向无环图。

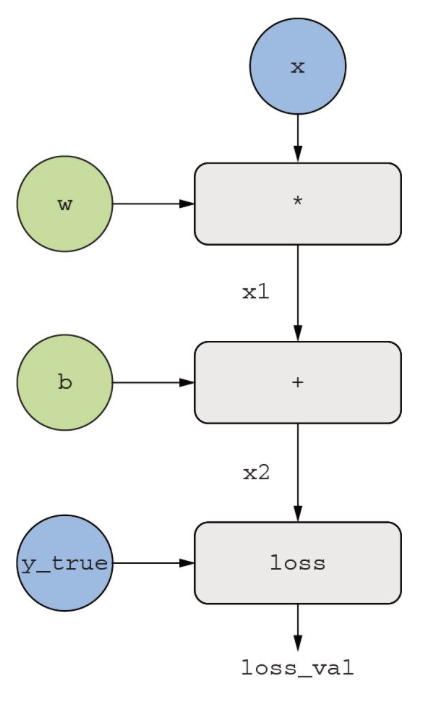
取两个标量变量 w 和 b，以及一个标量输入 x，然后对它们做一些运算，得到输出 y。最后，我们使用绝对值误差损失函数：$loss\underline{ }val = abs(y\underline{ }true - y)$。我们希望更新$w$和 $b$以使$loss\underline{ }val$最小化，所以需要计算 $grad(loss\underline{ }val, b)$ 和 $grad(loss\underline{ }val, w)$。

从上到下，直到获得$loss\underline{ }value$，这是向前传播的过程。

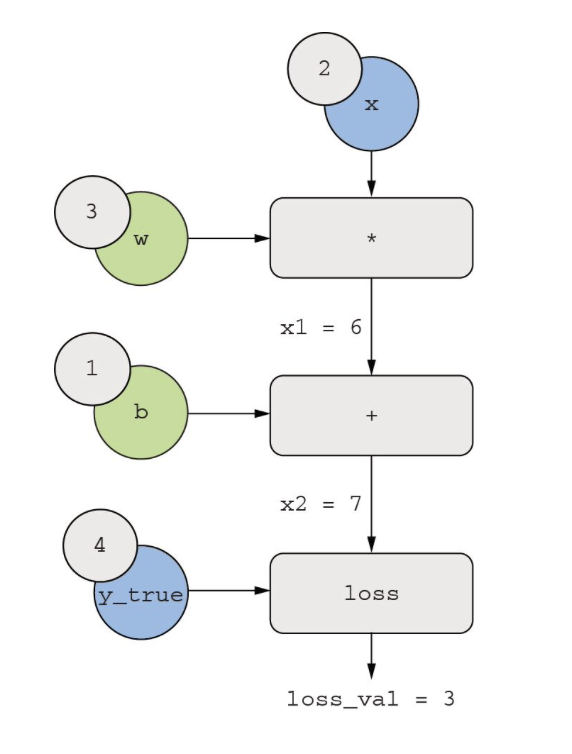
画出反向的边，表示反向传播的过程。

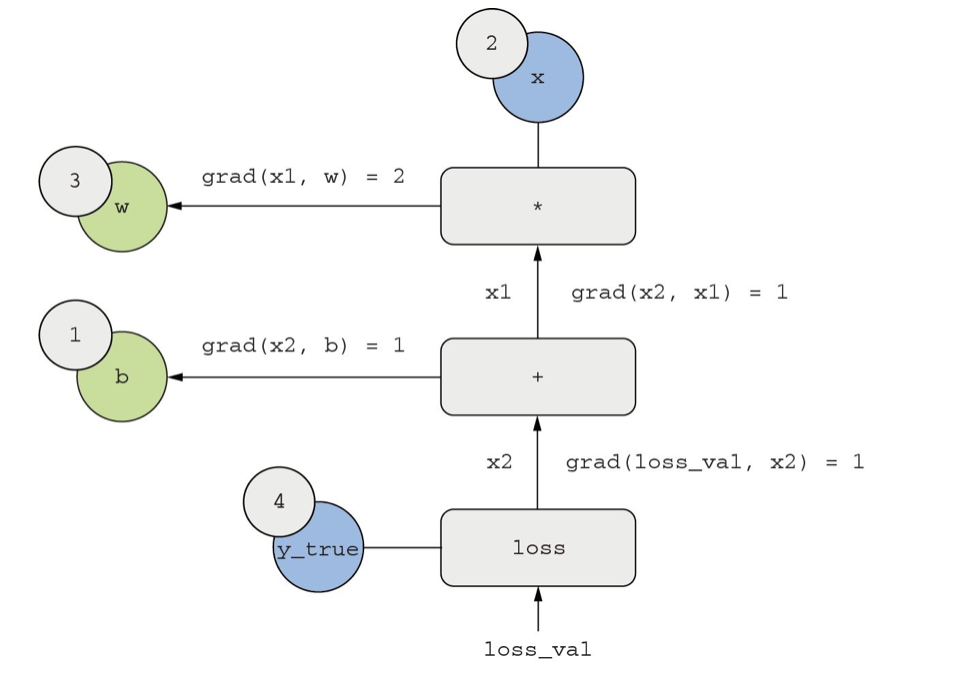
结果：

• grad(loss_val, x2) = 1，随x2变化一个小量epsilon, loss_val = abs(4 - x2) 的变化量相同。
• grad(x2, x1) = 1，随着x1变化一个小量epsilon，x2 = x1 + b = x1 + 1 的变化量相同。
• grad(x2, b) = 1，随着b变化一个小量epsilon, x2 = x1 +b = 6+ b的变化量相同。
• grad(x1, w) = 2，随着w变化一个小量epsilon，x1 = x w = 2 w的变化量为2倍的epsilon。

根据链式法则，对于反向图，想求一个节点相对于另一个节点的导数，将链接两个节点的路径上的每条边的导数相乘。

比如计算grad(loss, w) = grad(loss, x2) grad(x2, x1) grad(x1, w)

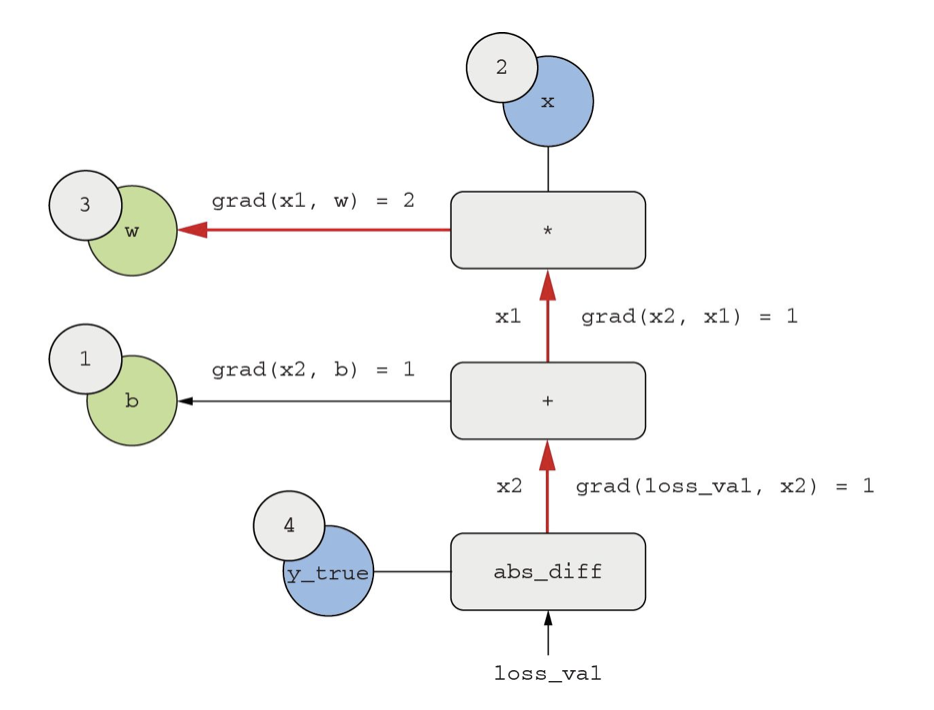
对应链式法则，得到想要的结果：

• grad(loss_val, w) = 1 1 2 = 2
• grad(loss_val,b) = 1*1 = 1

注意：在方向图中，如果a和b节点之间有多条路径，那么grad(a,b)等于所有路径值相加

03 TensorFlow的梯度带

GradientTape是一个API，进行自动微分。

import tensorflow as tf
x = tf.Variable(0.)  # 将标量Variable的值初始化为0
with  tf.GradientTape() as tape: #创建一个GradientTape作用域
    y = 2 * x +3  #在作用域内，对变量进行张量运算
    grad_of_y_wrt_x = tape.gradient(y,x) #利用梯度带获取输出y相对于变量x的梯度

张量运算

# GradientTape 也可以用于张量运算
x = tf.Variable(tf.zeros(2,2)) # 将Variable初始化为形状（2，2）的零张量
with tf.GradientTape() as tape:
    y = 2 * x + 3
grad_of_y_wrt_x = tape.gradient(y,x) #grad_of_y_wrt_x是一个形状为(2,2)的张量，与x相同
#表示y = 2 * x + 3 在x = [[0,0],[0,0]]附近的曲率

变量列表

# 适用于变量列表
W = tf.Variable(tf.random.uniform((2,2)))
b = tf.Variable(tf.zeros((2,)))
x = tf.random.uniform((2,2))
with tf.GradientTape() as tape:
    y = tf.matmul(x,W)+b # 在TensorFlow中matmul是指点积
grad_of_y_wrt_W_and_b = tape.gradient(y,[W,b]) #grad_of_y_wrt_W_and_b是由两个张量组成的列表
#这两个张量的形状分别于W和b相同
print(grad_of_y_wrt_W_and_b)